Tagawa Laboratory

概要

表面張力の温度依存性により表面張力勾配が駆動力となり生じる流れをマランゴニ対流 (Marangoni convection)といいます。これは熱対流の一種で、密度の温度依存性が原因となり発生する浮力対流（自然対流）とは対比的に捉えられますが、重力とは無関係に生じるところが特徴です。マランゴニ対流という用語は、イタリアの物理学者の名前にちなんでいます。

表面張力は、気液界面において界面接線方向に引っ張る力のことです。気液界面が平面のときには、この力を感じにくいですが、界面が曲率を持っていると実感できます。グラスに水を溢れそうなくらいに注いでも、持ちこたえて水がこぼれないのは表面張力によるためです。宇宙ステーション内のような微小重力環境では水滴は浮かんだ状態でほぼ球形になろうとしますが、これも表面張力によるものです。

表面張力は温度に依存します。通常、温度が高くなるほど表面張力は小さくなります。したがって自由表面に温度差がある場合には、高温側から低温側に引っ張られます。このように自由表面が移動することにより粘性力を介して内部まで流れが伝わり、結果としてマランゴニ対流が発生し、そして維持されます。

マランゴニ対流は、板ガラスの製造、フローティングゾーン法とよばれる半導体の単結晶育成法、相変化を伴う伝熱現象（凝縮や沸騰などの二相流）など様々な諸現象と関連します。最近、国際宇宙ステーションの微小重力環境を利用して、大直径の液柱マランゴニ対流の実験がなされました。大直径の液柱というのは重力下では作成困難ですし、複雑な振動流や乱流を呈しますので、数値解析の実行も容易ではありません。このように工業的応用と科学的解明の要請から、宇宙実験や大規模な数値計算などによって研究が行われています。

以下に、マランゴニ対流の代表的な例を紹介します。

Bénard-Marangoni対流

重力場において、下面から加熱され上面から冷却される水平流体層の浮力対流の安定性は、Rayleigh-Bénard問題として良く知られており、Chandrasekar の著書に詳述されています。20世紀初頭にBénardが鯨油を用いて行った実験では、上から眺めたときに多数の規則的な六角形の対流セル（Bénard セル）が観察されました。その実験では、流体層は浅く上面が自由界面である場合を扱っているので、今日では、浮力による影響よりはむしろ表面張力による影響がより支配的であったことがわかっています。

Pearsonは浮力がなくても表面張力勾配のみで水平液体層内に対流が発生することを初めて理論的に示しました。今日ではこれはBénard-Marangoni対流とよばれ、自由表面の熱的境界条件（ビオ数, Biot number）にも依存しますが、理論的にはマランゴニ数が臨界値の80以上にならないと対流は発生しないことが知られています。マランゴニ数（Marangoni number）は、以下のように定義されます。

\[ Ma = - \frac{(\partial \sigma/ \partial T)(T_1 - T_2)d}{\mu \alpha} \]

ここで、表面張力\(\sigma\) を温度\(T\)で微分した値（表面張力の温度係数）は通常負の値となりますが一定値とみなします。また\(T_1\)は固体面の温度を、\(T_2\)は自由表面の温度を表すものとします。この定義においては、\(Ma\)数が正になると液体層は不安定で、負になると安定です。固体面が冷却され自由表面が加熱される場合(\(T_1 < T_2\))には、\(Ma\)数は負ですから対流は発生しません。一方、(\(T_1 > T_2\))の場合には、臨界\(Ma\)数を超えると対流が発生し、\(T_2\)は自由表面上で温度変化を持ちますので、そうなるともはや上述の\(Ma\)数は定義できないことになります。

\(T_1 > T_2\)の場合に、対流が発生し臨界\(Ma\)数を定量的に議論するためには、線形安定性解析が必要です。しかしながら、そのような臨界値はさておき、なぜ不安定になるかということは定性的に理解することができます。興味のある方は、その理由を考えてみてください。

こちらはBénard-Marangoni対流の発生限界における可視化結果です。
\(Bi_{0}\rightarrow 0, Bi_{1}\rightarrow 0, Ma_{0} = 10000\)　の条件下においては、上面の臨界マランゴニ数\(Ma_{1c}\) = 139.92、およびその臨界波数 \(a_c\) = 2.90　と得られます。
ここで、\(Bi\)数とは境界面の物体の熱伝達率*代表長さ/熱伝導率であり、

\[ B_i = \frac{h d}{\lambda_b}\\ \]

と定義されます。

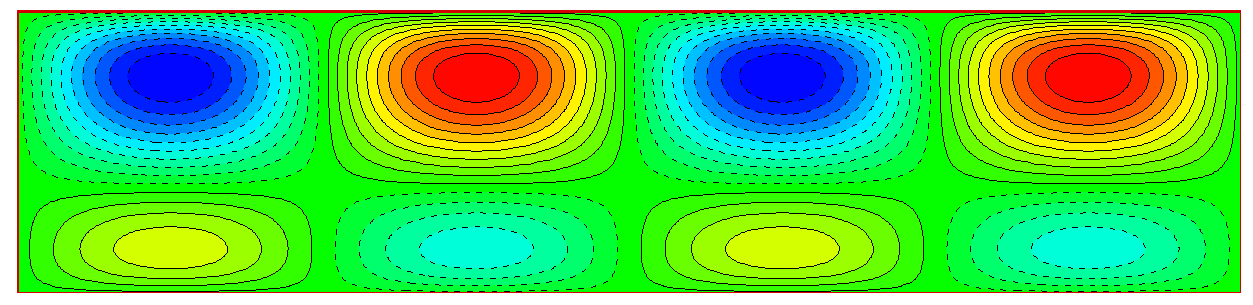
流れ関数

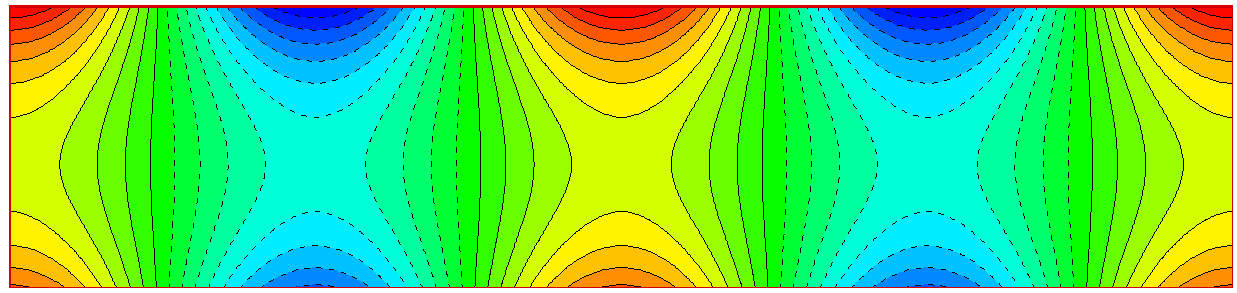
変動圧力

変動温度