自然対流
概要
自然対流は、地球表層の大気や海洋の流れなどの自然現象だけでなく、半導体の単結晶育成装置や原子炉の冷却などの工業施設にも見られる基本的な物理現象の一つであり、非常に重要なものです。これは、流体中に温度差があるときに、流体の密度差に起因して生じる熱輸送を伴う流れのことで、自然発生的に流れが起きるように見えることから自然対流(あるいは自由対流)と呼ばれます。通常、温められた部分は膨張し密度が小さくなるため、まわりの流体よりも相対的に軽くなって上昇します。一方で、冷やされた部分は収縮し密度が大きくなるため、そのまわりの流体よりも重くなって下降します。それらが駆動力となって流れが発生しますが、それが維持されるには温度差が保たれる何かの機構が必要になります。それがないと流体中の温度は対流と拡散により均一になろうとし、やがて流れは止まります。このように自然対流の発生原因は重力と温度差ですが、濃度差がある場合にも密度差が生じますので、対流が発生します。以下では、温度差に基づく場合を説明します。
本来、流体の密度は圧力と温度に依存して変化するので、以下のように表現できます。
\begin{eqnarray}
\rho(T,p) \simeq \rho(T_0,p_0)+\left( \frac{\partial \rho}{\partial T} \right)_0 (T-T_0) + \left( \frac{\partial \rho}{\partial p}\right)_0(p-p_0)
\end{eqnarray}
これは、体膨張係数βと等温音速cを用いて、近似的に
\[
\rho - \rho_0 = -\rho_0 \beta (T-T_0)+\frac{1}{c^2}(p-p_0)
\]
と書けます。一般に右辺第二項は、Mach数の小さい流れ(M << 1)においては右辺第一項と比べ無視できます。さらに、Boussinesq近似を用いれば、静圧分を差し引いた運動方程式(非圧縮性流れのNavier-Stokes方程式)は、以下のように書けます。
\[
\frac{\partial u_i}{\partial t}+\frac{\partial}{\partial x_j}(u_j u_i) = -\frac{1}{\rho_0}\frac{\partial p}{\partial x_i}
+ \nu \frac{\partial ^2 u_i}{\partial x_j \partial x_j} - g_i \beta (T-T_0)
\]
この方程式からわかるように、基準温度 \( T_0 \)よりも温度が高いか低いかに依存して、外力の向きが反転します。自然対流では、温度場と流れ場が相互に干渉しあうのに対し、強制対流では、浮力の影響を無視し、流れ場は温度場からの影響を受けないものとみなします。
以下は、古典的な研究例として、Rayleigh-Bénard対流について紹介します。
Rayleigh-Bénard対流
重力方向に直交するように置かれた無限に広い水平な平行平板間の流体層が下面から加熱され、上面から冷却される場合を考えます。この問題の場合、下面近傍の流体が軽くなって上昇しようとし、また上面近傍の流体は重くなって下降しようとするので、明らかに不安定で対流が容易に発生するように思われます。しかしながら、実際はある対流発生するための閾値を超えない限りにおいては、流体層は安定で熱伝導状態を維持するだけで流れはありません。この閾値は、流体層の厚さ\(d\)、重力加速度\(g\)、粘性係数\(\mu\)、密度\(\rho\)、熱伝導率\(k\)、比熱\(c_p\)、体膨張係数\(\beta\)、温度差\(\Delta T\)などに依存します。流体力学では、支配方程式を無次元化することで、これらの諸因子の組み合わせから成る無次元数を用いてより簡明に議論できることがよくあります。Reynolds数は最も良く知られた無次元数と云えるでしょう。このRayleigh-Bénard対流の場合には、Rayleigh数という無次元数が、対流発生限界の閾値を与えます。定義は以下の通りですが、慣性項を含まないNavier-Stokes方程式とエネルギー方程式を同時に無次元化すると現れます(ちなみに慣性項を含む場合だと、Rayleigh数とPrandtl数の両方が表れます。自然対流ではGrashof数という無次元数も良く用いられますが、これはRayleigh数をPrandtl数で割ったものです)。
\begin{eqnarray}
&&Ra &=& \frac{g \beta(\Delta T)d^3}{\alpha \nu}=\frac{\rho^2 c_p g \beta(\Delta T)d^3}{k \mu} \\
&& Pr &=& \frac{\nu}{\alpha} = \frac{\mu c_p}{k} \\
&& Gr &=& \frac{Ra}{Pr}
\end{eqnarray}
加熱面と冷却面がともに一定の温度で固定される場合には、線形安定性理論によれば、Rayleigh数が約1708を超えると流体層が不安定になり定常的な対流が発生することが知られています。加熱面が一定温度ではなく、一定の熱流束の場合には、より低い臨界値をとります。また、下側の平板が一定温度で加熱され、上側が自由表面で一定温度である場合には、臨界値は1100程度になることが知られています。詳しくは、下図のような横軸に無次元波数をとった中立安定曲線において、極小値をとる縦軸の値が臨界Rayleigh数となります。ここで無次元波数とは、対流セル幅に対する流体層の高さを表すものと考えて良いでしょう。円周率\(\pi\)で円形のセルになります。あまりに偏平な対流セルは起こりえず、円形に近い対流セルが起こりやすいことを示唆しています。

一定温度の場合

両面自由界面の場合

一面固体壁,一面自由界面の場合

両面固体壁の場合
・図はベクターグラフィックスとなっており、無限に拡大表示できます。
以下は線形安定性解析をしたときに得られる固有関数を可視化した図です。対流が起きる瞬間の様子となります。

Free-Free, \(k_c = 2.2214, Ra_c = 657.51\)
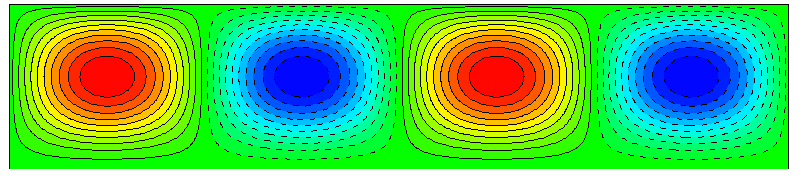
Free-Rigid, \(k_c = 2.682, Ra_c = 1100.65\)
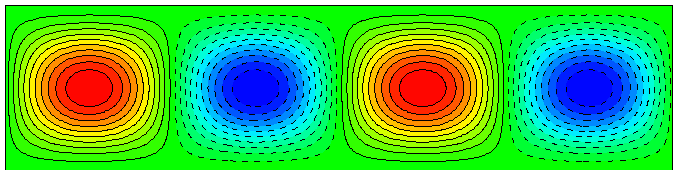
Rigid-Rigid, \(k_c = 3.116, Ra_c = 1707.76\)





