回転流体の安定性

流体の安定性において“流れ“とは定常な流れまたは時間的に周期をもつ流れをさし、これを基本流と呼びます。 流体が安定であるということは基本流に加わった撹乱が時間的または空間的に減衰することを意味します。流れが不安定ということはこの撹乱が成長することを意味します。 安定な流れと不安定な流れでは当然流れの挙動が異なるため、安定性と不安定性の臨界を求めることや不安定流れの挙動の解析は有用なものとなっています。

回転している流体を取り扱う回転流体では、流体とともに回転する座標系で解析を行う場合もあります。回転する流体にはコリオリ力や遠心力が働き、この力がほかの流れ場とは異なる流れを誘起する原因となっています。この特性を活かし、各種流体機械や化学反応装置に用いられることもあります。

田川研究室では回転流体としては「波動Taylor-Couette流」「回転軸傾斜による運動の評価」「自由表面を有する回転流体」「攪拌水槽内の流れ」などを研究しています。 不安定性としては「傾圧不安定波」を研究内容として、研究室内の勉強のために水平液体層の熱的不安定性を取り上げています。

回転流体の安定性ということで「傾圧不安定波」を少し紹介させて頂きます。

温度差をもった回転水槽内の流体は回転数や温度差がある閾値を超えると軸対称な流れが一変し、非軸対称な流れが形成されます。この非軸対称な流れは地球大気で観測される偏西風波動と呼ばれる現象と同じ原理で発生していて、偏西風波動の理解のために水槽モデルを使った実験、数値解析が行われています。 偏西風波動がなぜ発生するのかというと、回転を考慮しない場合、流体粒子は圧力差による力（気象学では気圧傾度力ともいう）によって等圧線を横切るように移動します。 しかし地球は回転しているため粒子は回転による力を受けて等圧線と平行に移動するようになります。 すると熱を移動させるはずの粒子がその働きを行えなくなるため、熱的不安定性が生じ大気が不安定になってしまいます。 この不安定性を解消するために波動を発生させることでその波動に伴って温度が拡散していくようになります。これが偏西風波動の発生メカニズムとなっています。 私たちは３次元直接数値計算や線形安定性理論を用いた解析を行っています。3次元直接数値計算の結果としては下図のような結果を得ています。 動画としてみたい方はLaboratoryのResult内にありますのでご覧ください。

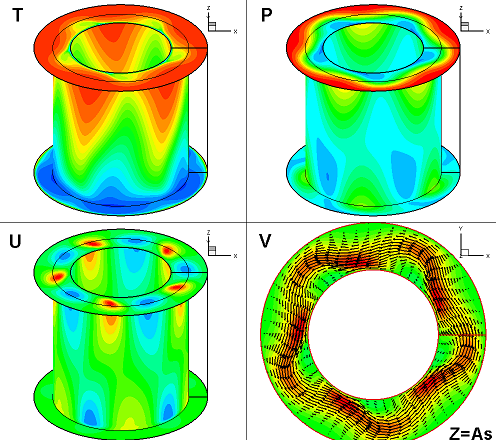
図1 傾圧不安定波